Circle Inequalities

For 0 < θ < π/2:
         (1 + sinθ)²
      > [(1/θ) cosθ + (1 + (π/2)/θ) sinθ] sinθ
      > (1/θ) cosθ sinθ (1 + sinθ)
      > (1/θ) cosθ sinθ
      > cos²θ
      > (1/θ) cosθ sinθ (1 − sinθ)
      > [(1/θ) cosθ + (1 − (π/2)/θ) sinθ] sinθ
      > (1 − sinθ)²

At the lower limit, θ = 0, all of the above inequalities become equalities (with all terms equal to 1). At the upper limit, θ = π/2, all of the terms except for the first two become equal to 0 (the first term become equal to 4, and the second becomes equal to 2).

Derivation:

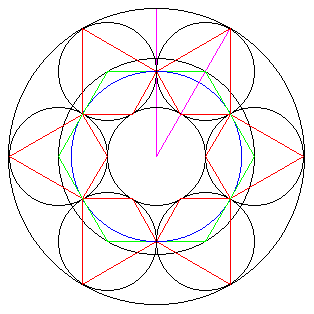
Consider an annulus enveloping n tangential circles. In the above diagram, where n=6, there are several sets of lines that are distinguished by colour:

The black lines form the n tangential circles, the two circles that form the annulus, and the circle that runs through the centre of each of the n circles. This latter circle lies midway between the two circles that form the annulus.
The blue line describes the circle that joins the tangential points of the n circles, and lies within the midway circle.
The green lines join the centres of the n circles with straight lines, forming tangents to the blue circle. Put together, they therefore form a regular n-sided polygon.
The red lines, within each of the n circles, form quadrilaterals joining the four points where the annulus and neighbouring circles meet the curve of the given circle.
The magenta lines mark off a sector of the diagram for closer examination, containing 1/(2n) of the entire diagram.

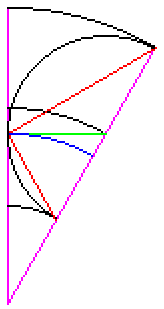
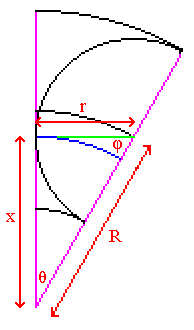Let θ be the angle between the magenta lines, and φ be its complement. (Note that all angles here are measured in circular measure; ie 2π radians form a complete revolution.)

Let R be the radius of the midway circle, r be the radius of each of the n tangential circles, and x be the radius of the blue circle. (So that the annulus is formed by two circles of radius R+r and R−r.)

Within the sector these form a right-angled triangle, giving the relationships:

      θ = (2π)/(2n) = π/n
      φ = π/2 − θ = π(n−2)/(2n)

      cos φ = sin θ
      sin φ = cos θ

      r = R sin θ = R sin (π/n)
      x = R cos θ = R cos (π/n)

Area contained by outer ring of annulus:
      [A circle of radius (R + r)]
      = π (R + r)²
      = π R² (1 + sinθ)²

Area contained by the epicycloid-like shape formed by the outside of the n tangential circles:
      [2n right-angled triangles with sides x and r, and 2n (π − φ) 2πths of a circle with radius r]
      = {2n × ½ xr} + {(2n) (π−φ) / (2π) × π r²}
      = nxr + n (π−φ) r²
      = n (R cosθ) (R sinθ) + n (1 − (n−2)/2n) π R² sin²θ
      = n R² cosθ sinθ + ½(n+2) π R² sin²θ
      = R² [n cosθ + (1 + ½n) π sinθ] sinθ

Area contained by the outer red polygon:
      [2n triangles with sides x and (R + r) and interior angle θ]
      = 2n × ½ x (R + r) sinθ
      = n (R cosθ) R (1 + sinθ) sinθ
      = n R² cosθ sinθ (1 + sinθ)

Area contained by midway circle:
[A circle of radius R]
= π R²

Area contained by the green polygon:
      [2n right-angled triangles with sides x and r]
      = 2n × ½ xr
      = n (R cosθ) (R sinθ)
      = n R² cosθ sinθ

Area contained by blue circle:
      [A circle of radius x]
      = π x²
      = π R² cos²θ

Area contained by the inner red polygon:
      [2n triangles with sides x and (R − r) and interior angle θ]
      = 2n × ½ x (R − r) sinθ
      = n (R cosθ) R (1 − sinθ) sinθ
      = n R² cosθ sinθ (1 − sinθ)

Area contained by the hypocycloid-like shape formed by the inside of the n tangential circles:
      [2n right-angled triangles with sides x and r, less 2n φ 2πths of a circle with radius r]
      = {2n × ½ xr} − {(2n) φ / (2π) × π r²}
      = nxr − nφ r²
      = n (R cosθ) (R sinθ) − n (n−2)/2n π R² sin²θ
      = n R² cosθ sinθ − ½(n−2) π R² sin²θ
      = R² [n cosθ + (1 − ½n) π sinθ] sinθ

Area contained by inner ring of annulus:
      [A circle of radius (R − r)]
      = π (R − r)²
      = π R² (1 − sinθ)²

From the diagrams, you can see that the areas of each of these shapes nest within each other (excepting the midway circle). This gives rise to the following series of inequalities:
         π R² (1 + sinθ)²
      > R² [n cosθ + (1 + ½n) π sinθ] sinθ
      > n R² cosθ sinθ (1 + sinθ)
      > n R² cosθ sinθ
      > π R² cos²θ
      > n R² cosθ sinθ (1 − sinθ)
      > R² [n cosθ + (1 − ½n) π sinθ] sinθ
      > π R² (1 − sinθ)²

Dividing each of the above by πR² gives the original inequalities. Clearly, although the diagram above uses an integer value for n, the inequalities still hold for all real n greater than 2. (Instead of considering a complete annulus containing n circles, consider the sector diagram above, and alter the value of θ accordingly.)

Taking the limit as n → ∞, keeping R constant, gives r = R sin(π/n) → 0. As such, the outer and inner circles forming the annulus meet, and all of the above inequalities necessarily become equalities. Taking the limit as n → 2, keeping R constant, gives r = R sin(π/n) → R. At this point, most of the above areas have shrunk into a point at the centre of the annulus, leaving only two tangential circles placed along the diameter of the outer circle of the annulus.

Note from the diagram that the inner red polygon is a scaled down copy of the outer red polygon. In particular, note that the two red lines within the sector diagram meet at a right angle. The inner red polygon rests between the inner ring of the annulus and the blue circle, and the outer red polygon rests between the blue circle and the outer ring of the annulus. It would appear, then, that:
      x / (R−r) = (R+r) / x
      x² = (R+r) (R−r)
      x² = R² − r²
      R² cos²θ = R² − R² sin²θ
      cos²θ + sin²θ = 1
...which holds for all θ. The area of the outer red polygon should also be x²/(R−r)² (or equivalently (R+r)²/x²) times larger than that of the inner red polygon:
      = n R² cosθ sinθ (1 − sinθ) × x²/(R−r)²
      = n R² cosθ sinθ (1 − sinθ) × cos²θ / (1 − sinθ)²
      = n R² cosθ sinθ (1 − sinθ) × (1 − sin²θ) / (1 − sinθ)²
      = n R² cosθ sinθ (1 − sinθ) × (1 + sinθ)(1 − sinθ) / (1 − sinθ)²
      = n R² cosθ sinθ (1 + sinθ)
...as required.